avatar NullAqua's Blog

NullAqua的个人博客

  • 首页
  • 分类
  • 标签
  • 归档
  • 关于
首页 Hash&KMP
文章

Hash&KMP

发表于 2022/11/30 更新于 2024/11/25
作者 NullAqua
17 分钟阅读
Hash&KMP
Hash&KMP

Hash

哈希表

OI-WIKI

哈希冲突

1. 开散列法

在遇到$hash$值相同的不同$key$值时,通过邻接表存储所有$key$值.

  • 优点: 实现简单方便
  • 缺点: 在使用时,需要根据情况动态开空间

2. 闭散列法

在遇到$hash$值相同的不同$key$值时,向后寻找未被使用的$hash$值,存入$key$值

  • 优点: 在使用过程中,不需要再开更多空间
  • 缺点: 实现较为麻烦

题目: Acwing137. 雪花雪花雪花

思路: 开一个set,记录雪花出现情况,枚举同一个雪花的不同形态,在set查询。若没找到,再插入当前雪花,时间复杂度$O(12nlogn)$,(使用unordered_set时间复杂度为$O(12n)$但常熟较大且实现困难,使用set更好)

0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77

#include<bits/stdc++.h>

using namespace std;
typedef long long ll;
typedef unsigned long long ull;


struct Node
{
    int a[6]{};

    bool operator<(const Node &o) const
    {
        for (int i=0;i<6;i++)
        {
            if (a[i]!=o.a[i])
            {
                return a[i]<o.a[i];
            }
        }
        return false;
    }

    bool operator==(const Node &o) const
    {
        for (int i=0;i<6;i++)
        {
            if (a[i]!=o.a[i])
            {
                return false;
            }
        }
        return true;
    }
};

set<Node> st;

Node get(Node &s,int i,int d)
{
    Node res;
    for (int &j:res.a)
    {
        j=s.a[i];
        i+=d;
        i=(i+6)%6;
    }
    return res;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n;
    cin>>n;
    for (int i=1;i<=n;i++)
    {
        Node s;
        for (int &j:s.a)
        {
            cin>>j;
        }
        for (int j=0;j<6;j++)
        {
            if (st.find(get(s,j,1))!=st.end()||st.find(get(s,j,-1))!=st.end())
            {
                cout<<"Twin snowflakes found.";
                return 0;
            }
        }
        st.insert(s);
    }
    cout<<"No two snowflakes are alike.";
    return 0;
}

树哈希

注意OIWiki上的三种树$hash$方法全是错的，都已经被Hack。

正确的树$hash$：

  • 子树按$hash$值排序 + 括号序字符串$hash$合并

题目: Acwing157. 树形地铁系统

思路: 计算2颗数的$hash$,判断是否相同,时间复杂度$O(nlogn)$

0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;

char tree[3005];
ull base[3005];
int ed;

pair<ull,int> getHash()
{
    ull hsh=1;
    vector<pair<ull,int>>vec;
    while (tree[++ed]=='0')
    {
        vec.push_back(getHash());
    }
    sort(vec.begin(),vec.end());
    int x=1;
    int sz=2;
    for (auto p:vec)
    {
        sz+=p.second;
        hsh=hsh*base[x]+p.first;
        x=p.second;
    }
    hsh=hsh*3+2;
    return make_pair(hsh,sz);
}

int main()
{
    base[0]=1;
    for (int i=1;i<=3000;i++)
    {
        base[i]=base[i-1]*3;
    }

    int n;
    cin>>n;
    for (int i=1;i<=n;i++)
    {
        memset(tree,'1',sizeof tree);
        tree[0]='0';
        cin>>(tree+1);
        ed=0;
        ull hsh=getHash().first;
        memset(tree,'1',sizeof tree);
        tree[0]='0';
        cin>>(tree+1);
        ed=0;
        ull hash1=getHash().first;
        if (hsh==hash1)
        {
            cout<<"same\n";
        }
        else
        {
            cout<<"different\n";
        }
    }
    return 0;
}

题目: P8499 [NOI2022] 挑战 NPC Ⅱ

思路: 先计算出$G$和$H$的每个子树的$hash$,对于树$G$中的一个节点$u_1$找到一个在$H$中对应的点$u_2$,将$u_2$ 的所有孩子为根的子树的$hash$值放入一个集合$U$中.枚举$u_1$的每个孩子$v$,若$U$中包含以$v$为根的树的$hash$值,则删去,若$U$中不包含,放入$U0$.若操作结束后$U$中元素比$U0$多,则无解。否则,尝试让$U0$与$U$中元素两两配对,对于$U0$ 中无法配对的元素,全部删去,配对后再递归执行上述比较。对于$U0$中元素个数$>k$的情况,则要么需要删去的点的数量$>k$,要么不可能达到目标,一定无解。否则,因为$k\leq5$则可以直接枚举每种匹配情况,最多$k!$种情况。

树$hash$时间复杂度$O(nlogn)$,执行上述匹配,时间复杂度$O(nk!)$,总时间复杂度$O(nk!)$

代码:

0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
typedef unsigned long long ull;

int fa[2][500005];
vector<int> adj[2][500005];
ull base[1000005];
ull hsh[2][500005];
int siz[2][500005];
int root[2];

int n[2];
int k;

void read(int kk)
{
    cin>>n[kk];
    for (int i=1;i<=n[kk];i++)
    {
        cin>>fa[kk][i];
        if (fa[kk][i]!=-1)
        {
            adj[kk][fa[kk][i]].push_back(i);
        }
        else
        {
            root[kk]=i;
        }
    }
}

void getHash(int kk,int u)
{
    hsh[kk][u]=1;
    siz[kk][u]=1;
    vector<pair<ull,int>> vec;
    for (int v:adj[kk][u])
    {
        getHash(kk,v);
        vec.emplace_back(hsh[kk][v],siz[kk][v]);
        siz[kk][u]+=siz[kk][v];
    }
    sort(vec.begin(),vec.end());
    for (auto p:vec)
    {
        hsh[kk][u]=hsh[kk][u]*base[p.second<<1]+p.first;
    }
    hsh[kk][u]=hsh[kk][u]*3+2;
}

pair<bool,int> compare(int u1,int u2,int mxk)
{
    if (hsh[0][u1]==hsh[1][u2])
    {
        return make_pair(true,0);
    }
    if (siz[0][u1]<=siz[1][u2]||adj[0][u1].size()<adj[1][u2].size())
    {
        return make_pair(false,0);
    }
    multimap<ull,int>mp;
    vector<int> vec;
    for (int v:adj[1][u2])
    {
        mp.emplace(hsh[1][v],v);
    }
    for (int v:adj[0][u1])
    {
        auto it=mp.find(hsh[0][v]);
        if (it!=mp.end())
        {
            mp.erase(it);
        }
        else
        {
            vec.push_back(v);
        }
    }
    if (vec.size()>mxk)
    {
        return make_pair(false,0);
    }
    vector<int> vec1;
    for (auto &p:mp)
    {
        vec1.push_back(p.second);
    }
    sort(vec.begin(),vec.end());
    sort(vec1.begin(),vec1.end());
    int ans=1e9;
    do
    {
        int cnt=0;
        bool flag=false;
        for (int i=0;i<vec1.size();i++)
        {
            auto p=compare(vec[i],vec1[i],mxk-cnt);
            if (!p.first)
            {
                flag=true;
                break;
            }
            else
            {
                cnt+=p.second;
            }
        }
        if (flag)
        {
            continue;
        }
        for (int i=(int)vec1.size();i<(int)vec.size();i++)
        {
            cnt+=siz[0][vec[i]];
        }
        ans=min(ans,cnt);
    }
    while (next_permutation(vec.begin(),vec.end()));
    return make_pair(ans<=mxk,ans);
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    base[0]=1;
    for (int i=1;i<=1000000;i++)
    {
        base[i]=base[i-1]*3;
    }
    int C,T;
    cin>>C>>T>>k;
    while (T--)
    {
        read(0);
        read(1);
        getHash(0,root[0]);
        getHash(1,root[1]);
        auto p=compare(root[0],root[1],k);
        cout<<(p.first?"Yes\n":"No\n");
        //clear
        for (int i=0;i<=max(n[0],n[1]);i++)
        {
            siz[1][i]=siz[0][i]=hsh[0][i]=hsh[1][i]=fa[0][i]=fa[1][i]=0;
            adj[0][i].clear();
            adj[1][i].clear();
        }
    }
    return 0;
}

更多资料：

  • AHU算法
  • Hash冲突的定量分析

字符串Hash

OI-WIKI

使用 unsigned long long自然溢出，或者双模数。

可以使用二分 + $Hash$的方法快速比较两个字符串的字典序。

Acwing138. 兔子与兔子

思路: $hash_r-hash_{l-1}*base^{len}$快速计算区间$hash$值,时间复杂度$O(n+m)$

0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
typedef unsigned long long ull;

char s[1000005];
ull hsh[1000005];
ull base[1000005];
int n;

ull getHash(int l,int r)
{
    int len=r-l+1;
    return hsh[r]-hsh[l-1]*base[len];
}

int main()
{
    cin>>(s+1);
    n=strlen(s+1);
    base[0]=1;
    for (int i=1;i<=n;i++)
    {
        hsh[i]=hsh[i-1]*27+s[i]-'a'+1;
        base[i]=base[i-1]*27;
    }
    int m;
    cin>>m;
    while (m--)
    {
        int l1,r1,l2,r2;
        cin>>l1>>r1>>l2>>r2;
        cout<<(getHash(l1,r1)==getHash(l2,r2)?"Yes\n":"No\n");
    }
    return 0;
}

Acwing139. 回文子串的最大长度

思路: 枚举回文中点,二分查找此中点能形成的最长回文串,使用$hash$进行check,时间复杂度$O(nlogn)$

0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
typedef unsigned long long ull;

ull hsh[2][1000005];
ull base[1000005]={1};
int n,ans;

ull getHash(int x,int l,int r)
{
    int len=abs(r-l)+1;
    return hsh[x][r]-hsh[x][l+(x?1:-1)]*base[len];
}

bool check(int x,int y)
{
    bool a1=getHash(0,x+1,x+y)==getHash(1,x-1,x-y);
    bool a2=getHash(0,x+1,x+y)==getHash(1,x,x-y+1);
    if (a1)
    {
        ans=max(ans,y<<1|1);
    }
    if (a2)
    {
        ans=max(ans,y<<1);
    }
    return a1||a2;
}

int find(int x)
{
    int ans=0;
    int l=1,r=min(x,n-x);
    while (l<=r)
    {
        int mid=(l+r)>>1;
        if (check(x,mid))
        {
            l=mid+1;
            ans=max(ans,mid);
        }
        else
        {
            r=mid-1;
        }
    }
    return ans;
}

int main()
{
    int T=0;
    for (int i=1;i<=1000000;i++)
    {
        base[i]=base[i-1]*27;
    }
    while (++T)
    {
        string x;
        cin>>x;
        n=x.length();
        if (x=="END")
        {
            return 0;
        }
        ans=1;
        memset(hsh[0],0,sizeof hsh[0]);
        memset(hsh[1],0,sizeof hsh[1]);
        for (int i=1;i<=n;i++)
        {
            hsh[0][i]=hsh[0][i-1]*27+x[i-1]-'a'+1;
        }
        for (int i=n;i>=1;i--)
        {
            hsh[1][i]=hsh[1][i+1]*27+x[i-1]-'a'+1;
        }
        for (int i=1;i<x.length();i++)
        {
            find(i);
        }
        cout<<"Case "<<T<<": "<<ans<<"\n";
    }
    return 0;
}

Acwing160. 匹配统计

思路: 枚举每个后缀,通过二分$hash$求出与$B$的的重复长度,之后$O(1)$回答询问,时间复杂度$O(nlogn)$

0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
typedef unsigned long long ull;

ull base[200005]={1};
int ans[200005];
ull hsh[2][200005];
string a,b;
int n,m;

bool check(int x,int y)
{
    return hsh[0][x+y-1]-hsh[0][x-1]*base[y]==hsh[1][y];
}

int find(int x)
{
    int l=0,r=min(n-x+1,m);
    int res=0;
    while (l<=r)
    {
        int mid=(l+r)>>1;
        if (check(x,mid))
        {
            l=mid+1;
            res=mid;
        }
        else
        {
            r=mid-1;
        }
    }
    return res;
}

int main()
{
    for (int i=1;i<=200000;i++)
    {
        base[i]=base[i-1]*27;
    }
    int q;
    cin>>n>>m>>q>>a>>b;
    for (int i=1;i<=max(n,m);i++)
    {
        if (i<=n)
        {
            hsh[0][i]=hsh[0][i-1]*27+a[i-1];
        }
        if (i<=m)
        {
            hsh[1][i]=hsh[1][i-1]*27+b[i-1];
        }
    }
    for (int i=1;i<=n;i++)
    {
        ans[find(i)]++;
    }
    while (q--)
    {
        int x;
        cin>>x;
        cout<<ans[x]<<'\n';
    }
    return 0;
}

KMP

OI-WIKI

Acwing141. 周期

思路: 一个字符串$S$的最短循环节长度应是$|S|-|border|$($S$长度减去$border$长度),并且循环节长度需要$|S|$的因数.

证明: 一个字符串$S$的最短循环节长度应是$|S|-|border|$

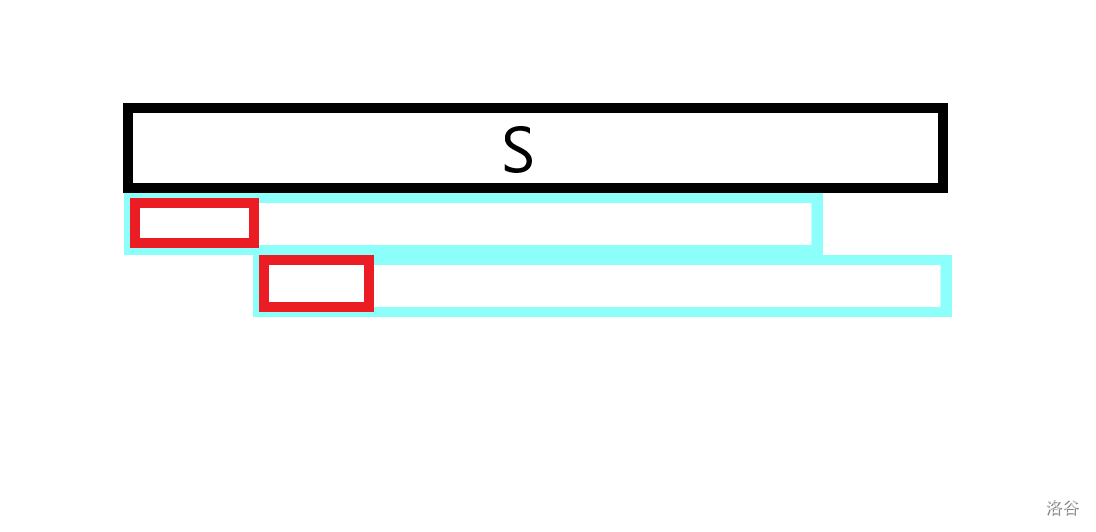
  1. $S[1 ~ (|S|-某个匹配的前后缀的长度)]$一定是一个循环节

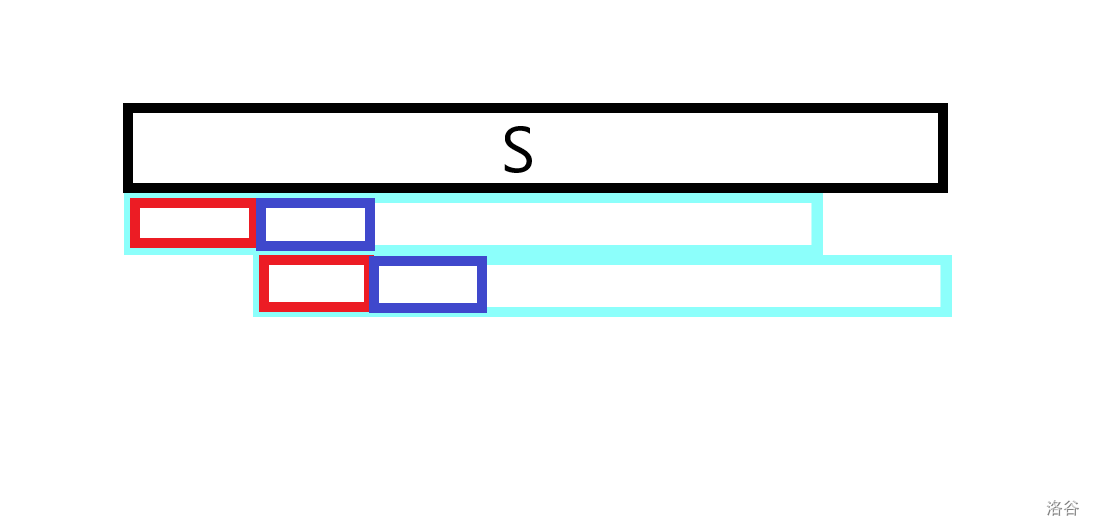
    如图,假设匹配的前后缀是蓝色部分,红色部分则是循环节,因为两个蓝色部分相等,则后缀中的红色部分等于前缀中的红色部分

    显然,前缀中的深蓝部分等于后缀中的红色部分,而后缀中的深蓝部分等于前缀中的深蓝部分,以此类推,可以证明第2段(深蓝色)等于第1段(红色),第3段等于第2段(深蓝色)…直到结束,所以$S[1 ~ (|S|-某个匹配的前后缀的长度)]$一定是一个循环节

  2. 循环节一定是$S[1 ~ (|S|-某个匹配的前后缀的长度)]$

    设循环次数为$K$,则第1 ~ (K-1)个循环节应与第2~K个循环节相同,则1 ~ (K-1)为匹配的前缀,2 ~ K为后缀

  3. 匹配的前后缀越长,|S|-其长度越小,即循环节最小。因为$border$是最长的匹配的前后缀,所以$|S|-|border|$是最短循环节

  4. 为什么不可能是$border$的$border$:因为$border$是最长的前后缀,所以$1$中的红色部分是最短的循环节,若不是,例如红色部分是由2个更小的循环节组成,则前后缀长度可以增长更小循环节的长度,不满足$border$的定义。而循环节只能是由若干个最短循环节组成的(否则,它们长度的最大公因数也将会是循环节,这就找到了更小循环节),所以若最短的循环节都不是$|S|$的因数,则其他循环节一定不是。而找$border$的$border$找到的循环节一定不会比最短循环节短

时间复杂度$O(n)$

代码:

0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
typedef unsigned long long ull;

int n;
string s;
int nxt[1000005];

void getNext()
{
    nxt[1]=0;
    for (int i=2,j=0;i<=n;i++)
    {
        while (j>0&&s[i]!=s[j+1])
        {
            j=nxt[j];
        }
        if (s[i]==s[j+1])
        {
            j++;
        }
        nxt[i]=j;
    }
}

int main()
{
    int T=0;
    while ((cin>>n)&&n)
    {
        cin>>s;
        s=' '+s;
        T++;
        cout<<"Test case #"<<T<<'\n';
        getNext();
        for (int i=2;i<=n;i++)
        {
            if (i%(i-nxt[i])==0&&nxt[i]!=0)
            {
                cout<<i<<' '<<i/(i-nxt[i])<<'\n';
            }
        }
        cout<<'\n';
    }
    return 0;
}

Acwing159. 奶牛矩阵

思路: 枚举覆盖子矩阵的宽度,对于一个宽度$d$,可以将整个区间切成若干个$R*d$的矩阵,通过$hash$ 快速判断这些矩阵是否相同。若相同,再在竖直方向上,依据横向的$hash$值做$kmp$匹配,求出循环节,时间复杂度$O(CR+C^2)$

代码:

0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
typedef unsigned long long ull;

int n,m;
string s[80];
ull base[10005]={1};
ull hsh[2][10005][80];
int nxt[10005];

void getNext(int x)
{
    nxt[1]=0;
    for (int i=2,j=0;i<=n;i++)
    {
        while (j>0&&hsh[0][i][x]!=hsh[0][j+1][x])
        {
            j=nxt[j];
        }
        if (hsh[0][i][x]==hsh[0][j+1][x])
        {
            j++;
        }
        nxt[i]=j;
    }
}

void getHash()
{
    for (int i=1;i<=n;i++)
    {
        for (int j=1;j<=m;j++)
        {
            hsh[0][i][j]=hsh[0][i][j-1]*27+s[j][i]-'A'+1;
        }
    }
    for (int i=1;i<=n;i++)
    {
        for (int j=1;j<=m;j++)
        {
            hsh[1][i][j]=hsh[1][i-1][j]*27+s[j][i]-'A'+1;
        }
    }
}

int main()
{
    for (int i=1;i<10000;i++)
    {
        base[i]=base[i-1]*27;
    }
    cin>>n>>m;
    for (int i=0;i<=n;i++)
    {
        for (int j=1;j<=m;j++)
        {
            if (!i)
            {
                s[j]+=' ';
                continue;
            }
            char ch;
            cin>>ch;
            s[j]+=ch;
        }
    }
    int ans=1e9;
    getHash();
    for (int d=1;d<=m;d++)
    {
        bool flag=false;
        for (int i=1;i<=m;i++)
        {
            if (hsh[1][n][(i-1)%d+1]!=hsh[1][n][i])
            {
                flag=true;
                break;
            }
        }
        if (flag)
        {
            continue;
        }
        getNext(d);
        ans=min(ans,d*(n-nxt[n]));
    }
    cout<<ans<<'\n';
    return 0;
}

最小表示法

OI-Wiki

Acwing158. 项链

思路: 求出$2$个字符串的最小表示,然后判断$2$个字符串的最小表示是否相同,时间复杂度$O(n)$

0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned __int128 uint128;

string a,b;

int get(string &xx)
{
    string x=' '+xx+xx;
    int n=xx.length();
    int i=1,j=2,k;
    while (i<=n&&j<=n)
    {
        for (k=0;k<n&&x[i+k]==x[j+k];k++);
        if (k==n)
        {
            break;
        }
        if (x[i+k]>x[j+k])
        {
            i=i+k+1;
            if (i==j)
            {
                i++;
            }
        }
        else
        {
            j=j+k+1;
            if (i==j)
            {
                j++;
            }
        }
    }
    return min(i,j);
}

int main()
{
    cin>>a>>b;
    int x=get(a)-1;
    int y=get(b)-1;
    string res="Yes\n";
    for (int i=0;i<a.length();i++)
    {
        if (a[(x+i)%a.length()]!=b[(y+i)%b.length()])
        {
            cout<<"No";
            return 0;
        }
        res+=a[(x+i)%a.length()];
    }
    cout<<res;
    return 0;
}
develop, cpp
信息作业
本文由作者按照 CC BY-NC 4.0 进行授权, 未经许可不得转载。
分享

最近更新

  • FuckBrainfuck
  • Java快速入门指南
  • Hash&KMP
  • c++快读快写
  • Kotlin序列化多态

热门标签

develop kotlin cpp工具 java 信息作业

外部链接

  •  此博客的 Github 仓库
  •  此博客的评论仓库

文章内容

相关文章

2023/03/26

c++快读快写

c++快读快写 cin换成in,cout换成out,cerr换为err 输出换行:out&lt;&lt;endln err&lt;&lt;endln 输出清空缓存(flush): out&lt;&lt;flush err&lt;&lt;flush (不手动清理则在程序结束时自动清理) get line:string s;in.getline(s);或char s[1000...

2024/11/28

FuckBrainfuck

FuckBrainfuck 先叠甲 以下内容纯属娱乐，不具有任何实际意义。我无法保证我的实现没有问题，如有问题欢迎指出。 Brainfuck简述 若你已经知道何为Brainfuck,请跳过此部分. Brainfuck是一种极简单的编程语言,由Urban Müller于1993年创造。它只包含八个命令，分别是&gt; &lt; + - [ ] . ,。它的内存模型是一个无限长度的字节数...

2024/11/25

Kotlin序列化多态

Kotlin序列化多态 关于Kt多态简述 当在序列化中出现多态时，会在序列化结果中带上类判别器（classDiscriminator），以区分不同的class。默认为type，并且可以通过classDiscriminator修改。也可以通过classDiscriminatorMode修改何时添加判别器 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 1...

-

c++快读快写

© 2024 NullAqua. 保留部分权利。

|

本站采用 Jekyll 主题 Chirpy

热门标签

develop kotlin cpp工具 java 信息作业

发现新版本的内容。